Tuning Frequncies

25 Oct 2015

Most recently, I attacked an interesting task: tuning a raw frequency to the nearest note.

First, you have to know a few things about the equal-tempered chromatic scale:

There are 12 notes in every octave.
A note that is one octave higher than another note will have twice the frequency.
So, to move up one chromatic note, you multiply the current note by the twelth root of 2.

Knowing this, we can write this equation:

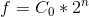
where:

f is the raw frequency (this is the input to the function)
C₀ is the frequency of the lowest note, 16.35
n is the amount of doubling required.

This equation can be solved for n:

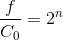
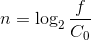
Since we know that every time a note doubles the octave increases once, the integer part of n must be equal to the octave.

Since we know there are twelve notes in an octave, we determine which note in the scale the raw frequency represents by multiplying the decimal by 12.

Taking this all into account, I came up with the following method:

import math

def tune(f):
    # constant frequency of lowest C
    # based off an instrument tuned to A4 == 440 Hz
    C0 = 16.35
    # each scale starts with a C
    NOTE_NAMES = ["C","C#","D","D#","E","F","F#","G","G#","A","A#","B"]
    # calculate and return the note and octave
    n = math.log(f/C0, 2)
    note = int(round(n%1*12, 0))
    octave = int(n)
    return NOTE_NAMES[note] + str(octave)

Then, I wanted to be sure I made no mistakes, so I found a chart of all the frequencies of the equal-tempered chromatic scale and wrote a few test cases. If you run the following test, you will see that the tuning function works perfectly.

if __name__ == "__main__":
    # test the tuning function
    assert tune(27.50) == "A0"
    assert tune(45) == "F#1"
    assert tune(440) == "A4"
    assert tune(2489.5) == "D#7"
    print("tuner tested successfully")

Algorithmic Musician

Senior project for the procedural generation of music

Tuning Frequncies